Many people enjoy chess, and with its popularity, chess has a major online presence, and dozens of famous variations of the game, like Bughouse and Losing Chess. While researching for my last post on the Magic the Gathering Turing Machine, I found both a Youtube video and a paper (by C.D.A. Evans and Joel David Hamkins) describe a unique variant of chess, one with a large board, infinite in size in every direction. Today I’ll explain checkmate, ordinals, and how a set of pieces can represent infinity.

Checkmate in Infinite chess

For those who don’t play chess, checkmate is the end result of the game, where a king is unable to move to a situation where they will not get captured the next turn. In the example below, the pawn attacks the king, and the edges of the board along with the bishop prevents the king from moving.

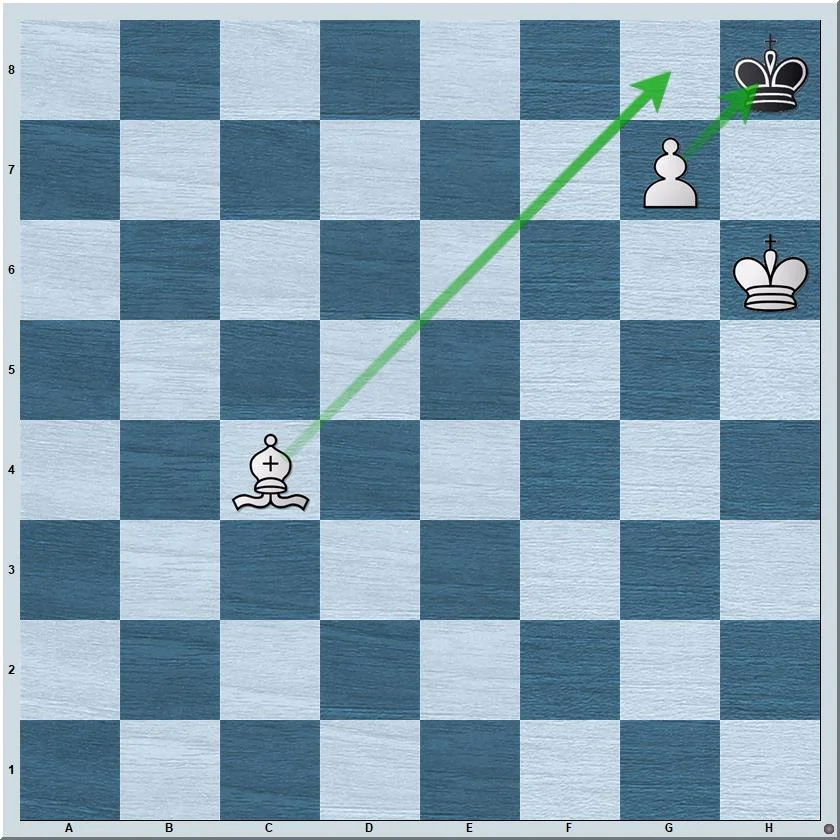
Example of checkmate

However, in infinite chess, the board cannot restrict movement; when a piece has an unobstructed path, they can pick a direction and a number n, and then move that many spaces in that direction. This means an unblocked rook could move 2, 50, or 1,005,688,288,434 spaces to the right, and still be on the board.

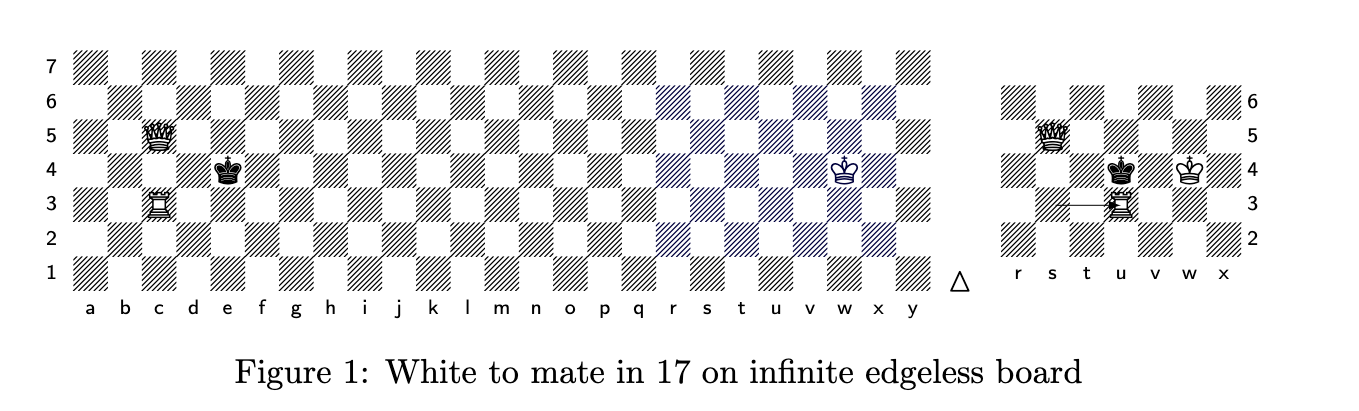
An example of Checkmate-in-N is the diagram below, taken from the paper: Example of checkmate

The black king can only move to the right to avoid mate, and the queen and rook will follow, eventually mating when the kings are almost touching. In this case, if each side plays optimally , the game will always end within N moves, where N is the distance between the kings.

Time for Mate in ω

Mate in ω can be thought of “Schrödinger’s” mate; you know it will result in checkmate, but given a position, you could have a mate-in-1, a mate-in-2… as high as you want based on the next move played:

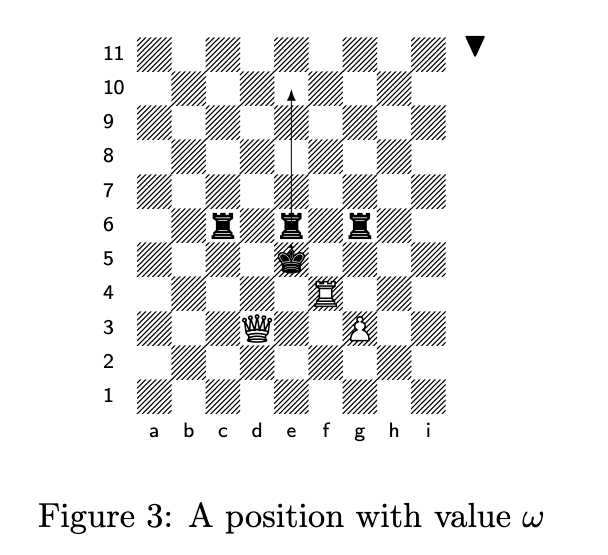
Example of checkmate in omega

Black is to move, and if they move the center rook, they have to choose how many places they want to move back since they are unbounded in that direction. However, immediately after the move is made, a countdown begins, and the white pieces will push the king to checkmate against it own rook, similar to the picture before.

Therefore, the researchers needed a naming convention that could encompass all the possible number of mates that could be triggered, and thus used ω, the ordinal infinity, the smallest number bigger than all the natural numbers.

why do we need this numbering system?

Omega is not like the infinities we know from calculus, where this infinity is simply bigger than everything but you can compare it to itself; omega is like the “biggest number” game children play:

“I double-dog dare you!”

“I triple-dog dare you!”

“I infinity-dog dare you!”

…After much thinking…

“I infinity and one-dog dare you!”

Omega is bigger than every natural number, but omega and one is “biggerer”, even more than regular omega. this means you get a hierarchy like this:

\[1 < 2 < 3 < ... < \omega < \omega + 1 < ... < 2*\omega < ... < \omega^2 < ... < \omega^{\omega}...\]

All of these values shown can be represented with chessboards; let’s show an example for $\omega^2$:

Example of checkmate in omega^2

To keep it short, let’s talk about the top left: we have a black rook in a channel surrounded by pawns, and the rook can move $\omega$ spaces away to delay the white pawns, where all the pawns on one side of the channel need to move to allow a rook on that side to checkmate. The funny part is the king-rook set on the right; every time a pawn moves, the rook leaps $\omega$ steps to the right, ready to annoy the white king with repeated checks for an ungodly amount of turns; only when the white king threatens capture of the rook is when the black rook leaps and a single white pawn moves (remember we have $\omega$ to deal with). This gives us $\omega^2$ turns until white ends the game.

Conclusion

Chess has evolved far past its legacy as the game of kings; it is also the game of mathematicians who plan on ruining matches until the end of time. Though its practical use is limited, infinite chess shows the greater maths community new ways to represent old concepts, hopefully in ways that allow more people to understand the craziness and usefulness of math.

Once again, please check out the original paper on transfinite chess. This post is meant to be a jumping off point, simplifying some aspects of the math to make it easier to understand.